26.1.13

Butterfly effect - Wikipedia

Butterfly effect - Wikipedia




In chaos theory, the butterfly effect is the sensitive dependence on initial conditions, where a small change at one place in a deterministic nonlinear system can result in large differences to a later state. The name of the effect, coined by Edward Lorenz, is derived from the theoretical example of a hurricane's formation being contingent on whether or not a distant butterfly had flapped its wings several weeks before.

Although the butterfly effect may appear to be an esoteric and unlikely behavior, it is exhibited by very simple systems: for example, a ball placed at the crest of a hill may roll into any of several valleys depending on, among other things, slight differences in initial position.

The butterfly effect is a common trope in fiction when presenting scenarios involving time travel and with hypotheses where one storyline diverges at the moment of a seemingly minor event resulting in two significantly different outcomes.

Contents

Origin of the concept and the term

Chaos theory and the sensitive dependence on initial conditions was described in the literature in a particular case of the three-body problem by Henri Poincaré in 1890.[1] He later proposed that such phenomena could be common, for example, in meteorology.[citation needed]

In 1898,[1] Jacques Hadamard noted general divergence of trajectories in spaces of negative curvature. Pierre Duhem discussed the possible general significance of this in 1908.[1] The idea that one butterfly could eventually have a far-reaching ripple effect on subsequent historic events first appears in "A Sound of Thunder", a 1952 short story by Ray Bradbury about time travel (see Literature and print here).

In 1961, Lorenz was using a numerical computer model to rerun a weather prediction, when, as a shortcut on a number in the sequence, he entered the decimal 0.506 instead of entering the full 0.506127. The result was a completely different weather scenario.[2] In 1963 Lorenz published a theoretical study of this effect in a well-known paper called Deterministic Nonperiodic Flow.[3] Elsewhere he said[citation needed] that "One meteorologist remarked that if the theory were correct, one flap of a seagull's wings could change the course of weather forever." Following suggestions from colleagues, in later speeches and papers Lorenz used the more poetic butterfly. According to Lorenz, when he failed to provide a title for a talk he was to present at the 139th meeting of the American Association for the Advancement of Science in 1972, Philip Merilees concocted Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas? as a title. Although a butterfly flapping its wings has remained constant in the expression of this concept, the location of the butterfly, the consequences, and the location of the consequences have varied widely.[4]

The phrase refers to the idea that a butterfly's wings might create tiny changes in the atmosphere that may ultimately alter the path of a tornado or delay, accelerate or even prevent the occurrence of a tornado in another location. Note that the butterfly does not power or directly create the tornado. The flap of the wings is a part of the initial conditions; one set of conditions leads to a tornado while the other set of conditions doesn't. The flapping wing represents a small change in the initial condition of the system, which causes a chain of events leading to large-scale alterations of events (compare: domino effect). Had the butterfly not flapped its wings, the trajectory of the system might have been vastly different - it's possible that the set of conditions without the butterfly flapping its wings is the set that leads to a tornado.

Illustration

The butterfly effect in the Lorenz attractor
time 0 ≤ t ≤ 30 (larger) z coordinate (larger)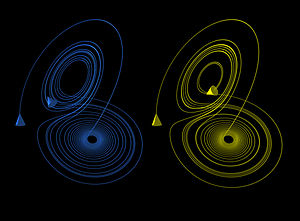
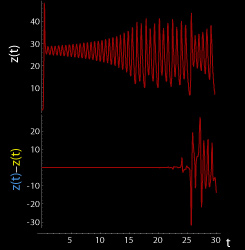
TwoLorenzOrbits.jpg LorenzCoordinatesSmall.jpg
These figures show two segments of the three-dimensional evolution of two trajectories (one in blue, the other in yellow) for the same period of time in the Lorenz attractor starting at two initial points that differ by only 10−5 in the x-coordinate. Initially, the two trajectories seem coincident, as indicated by the small difference between the z coordinate of the blue and yellow trajectories, but for t > 23 the difference is as large as the value of the trajectory. The final position of the cones indicates that the two trajectories are no longer coincident at t = 30.
A Java animation of the Lorenz attractor shows the continuous evolution.

Theory and mathematical definition

Recurrence, the approximate return of a system towards its initial conditions, together with sensitive dependence on initial conditions, are the two main ingredients for chaotic motion. They have the practical consequence of making complex systems, such as the weather, difficult to predict past a certain time range (approximately a week in the case of weather) since it is impossible to measure the starting atmospheric conditions completely accurately.

A dynamical system displays sensitive dependence on initial conditions if points arbitrarily close together separate over time at an exponential rate. The definition is not topological, but essentially metrical.

If M is the state space for the map 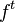f^t, then 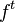f^t displays sensitive dependence to initial conditions if for any x in M and any δ > 0, there are y in M, with 0 < d(x, y) < \delta such that
d(f^\tau(x), f^\tau(y)) > \mathrm{e}^{a\tau} \, d(x,y).
The definition does not require that all points from a neighborhood separate from the base point x, but it requires one positive Lyapunov exponent.

Examples

The butterfly effect is most familiar in terms of weather; it can easily be demonstrated in standard weather prediction models, for example.[5]

The potential for sensitive dependence on initial conditions (the butterfly effect) has been studied in a number of cases in semiclassical and quantum physics including atoms in strong fields and the anisotropic Kepler problem.[6][7] Some authors have argued that extreme (exponential) dependence on initial conditions is not expected in pure quantum treatments;[8][9] however, the sensitive dependence on initial conditions demonstrated in classical motion is included in the semiclassical treatments developed by Martin Gutzwiller[10] and Delos and co-workers.[11]

Other authors suggest that the butterfly effect can be observed in quantum systems. Karkuszewski et al. consider the time evolution of quantum systems which have slightly different Hamiltonians. They investigate the level of sensitivity of quantum systems to small changes in their given Hamiltonians.[12] Poulin et al. presented a quantum algorithm to measure fidelity decay, which "measures the rate at which identical initial states diverge when subjected to slightly different dynamics." They consider fidelity decay to be "the closest quantum analog to the (purely classical) butterfly effect."[13] Whereas the classical butterfly effect considers the effect of a small change in the position and/or velocity of an object in a given Hamiltonian system, the quantum butterfly effect considers the effect of a small change in the Hamiltonian system with a given initial position and velocity.[14][15] This quantum butterfly effect has been demonstrated experimentally.[16] Quantum and semiclassical treatments of system sensitivity to initial conditions are known as quantum chaos.[8][14]

In popular culture

Main article: Butterfly effect in popular culture

See also

References

  1. ^ a b c Some Historical Notes: History of Chaos Theory
  2. ^ Mathis, Nancy (2007). Storm Warning: The Story of a Killer Tornado. Touchstone. p. x. ISBN [[Special:BookSources/0-7432-8053-2|0-7432-8053-2]].
  3. ^ Lorenz, Edward N. (March 1963). "Deterministic Nonperiodic Flow". Journal of the Atmospheric Sciences 20 (2): 130–141. Bibcode 1963JAtS...20..130L. doi:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2. ISSN 1520-0469. Retrieved 3 June 2010.
  4. ^ "The Butterfly Effects: Variations on a Meme". AP42 ...and everything. Retrieved 3 August 2011.
  5. ^ http://www.realclimate.org/index.php/archives/2005/11/chaos-and-climate/
  6. ^ Heller, E. J.; Tomsovic, S. (July 1993). "Postmodern Quantum Mechanics". Physics Today.
  7. ^ Gutzwiller, Martin C. (1990). Chaos in Classical and Quantum Mechanics. New York: Springer-Verlag. ISBN 0-387-97173-4.
  8. ^ a b Rudnick, Ze'ev (January 2008). "What is... Quantum Chaos" (PDF). Notices of the American Mathematical Society.
  9. ^ Berry, Michael (1989). "Quantum chaology, not quantum chaos". Physica Scripta 40 (3): 335. Bibcode 1989PhyS...40..335B. doi:10.1088/0031-8949/40/3/013.
  10. ^ Gutzwiller, Martin C. (1971). "Periodic Orbits and Classical Quantization Conditions". Journal of Mathematical Physics 12 (3): 343. Bibcode 1971JMP....12..343G. doi:10.1063/1.1665596.
  11. ^ Gao, J. & Delos, J. B. (1992). "Closed-orbit theory of oscillations in atomic photoabsorption cross sections in a strong electric field. II. Derivation of formulas". Phys. Rev. A 46 (3): 1455–1467. Bibcode 1992PhRvA..46.1455G. doi:10.1103/PhysRevA.46.1455.
  12. ^ Karkuszewski, Zbyszek P.; Jarzynski, Christopher; Zurek, Wojciech H. (2002). "Quantum Chaotic Environments, the Butterfly Effect, and Decoherence". Physical Review Letters 89 (17): 170405. arXiv:quant-ph/0111002. Bibcode 2002PhRvL..89q0405K. doi:10.1103/PhysRevLett.89.170405.
  13. ^ Poulin, David; Blume-Kohout, Robin; Laflamme, Raymond & Ollivier, Harold (2004). "Exponential Speedup with a Single Bit of Quantum Information: Measuring the Average Fidelity Decay". Physical Review Letters 92 (17): 177906. arXiv:quant-ph/0310038. Bibcode 2004PhRvL..92q7906P. doi:10.1103/PhysRevLett.92.177906. PMID 15169196.
  14. ^ a b Poulin, David. "A Rough Guide to Quantum Chaos" (PDF).
  15. ^ Peres, A. (1995). Quantum Theory: Concepts and Methods. Dordrecht: Kluwer Academic.
  16. ^ Lee, Jae-Seung & Khitrin, A. K. (2004). "Quantum amplifier: Measurement with entangled spins". Journal of Chemical Physics 121 (9): 3949. Bibcode 2004JChPh.121.3949L. doi:10.1063/1.1788661.
Posted by at